విషయము

• స్టెప్స్
• చిట్కాలు

గణిత శాస్త్రవేత్తలు మరియు గ్రాఫిక్స్ ప్రోగ్రామర్లు తరచుగా రెండు వెక్టర్ల మధ్య కోణాన్ని కనుగొనవలసి ఉంటుంది. అదృష్టవశాత్తూ, ఈ కోణాన్ని లెక్కించడానికి ఉపయోగించే సూత్రానికి సాధారణ స్కేలార్ ఉత్పత్తి కంటే మరేమీ అవసరం లేదు. రెండు-డైమెన్షనల్ వెక్టర్లను ఉపయోగిస్తున్నప్పుడు ఈ ఫార్ములా వెనుక ఉన్న తార్కికం అర్థం చేసుకోవడం సులభం అయినప్పటికీ, మనం దానిని ఎన్ని భాగాలతోనైనా వెక్టర్లకు సులభంగా స్వీకరించవచ్చు.

స్టెప్స్

2 యొక్క పార్ట్ 1: రెండు వెక్టర్స్ మధ్య కోణాన్ని లెక్కించండి

1. 

   రెండు వెక్టర్లను గుర్తించండి. రెండు వెక్టర్స్ గురించి తెలిసిన అన్ని సమాచారాన్ని రాయండి. ఈ ట్యుటోరియల్ యొక్క ప్రయోజనం కోసం, వెక్టర్స్‌ను వాటి డైమెన్షనల్ కోఆర్డినేట్‌ల పరంగా మాత్రమే మీకు తెలుసని మేము అనుకుంటాము (దీనిని కూడా పిలుస్తారు భాగాలు). మీకు ఇప్పటికే తెలిస్తే మాడ్యూల్ లేదా ప్రామాణిక ఈ వెక్టర్లలో (అంటే వాటి పొడవు), మీరు క్రింద ఉన్న కొన్ని దశలను దాటవేయవచ్చు.
   • ఉదాహరణ: మేము రెండు డైమెన్షనల్ వెక్టర్స్ = (2,2) మరియు = (0,3) ను పరిశీలిస్తాము. ఈ రెండు వెక్టర్లను = 2 గా తిరిగి వ్రాయవచ్చునేను + 2j e = 0నేను + 3j = 3j.
   • మా ఉదాహరణ రెండు రెండు డైమెన్షనల్ వెక్టర్లను ఉపయోగిస్తున్నప్పటికీ, మేము ఈ క్రింది సూచనలను ఎన్ని భాగాలతోనైనా వెక్టర్లకు వర్తింపజేయవచ్చు.

2. 

   
   
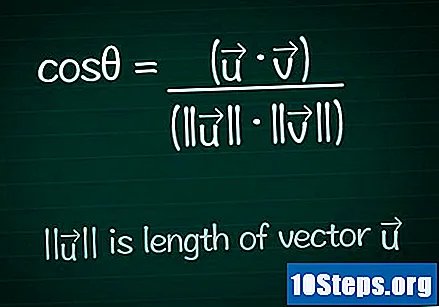
   కొసైన్ సూత్రాన్ని వ్రాయండి. ఏదైనా రెండు వెక్టర్ల మధ్య కోణం యొక్క విలువను కనుగొనడానికి, మనం మొదట ఆ కోణం యొక్క కొసైన్‌ను లెక్కించాలి. మీరు సూత్రాన్ని వివరంగా శోధించవచ్చు మరియు కనుగొనవచ్చు లేదా క్రింద ఉన్న విధంగా వ్రాయవచ్చు:
   • cosθ = (•) / (|||| ||||)
   • |||| సూచిస్తుంది మాడ్యూల్ (లేదా పొడవు) వెక్టర్ ".
   • • సూచిస్తుంది స్కేలార్ ఉత్పత్తి (లేదా అంతర్గత ఉత్పత్తి) రెండు వెక్టర్స్.

3. 

   
   
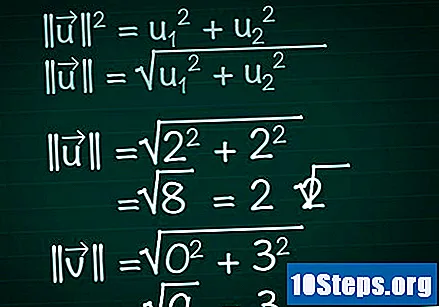
   ప్రతి వెక్టర్ యొక్క మాడ్యులస్ను లెక్కించండి. భాగం ద్వారా ఏర్పడిన కుడి త్రిభుజాన్ని g హించుకోండి x వెక్టర్ యొక్క, దాని భాగం y మరియు వెక్టర్ కూడా. ఈ త్రిభుజంలో, వెక్టర్ హైపోటెన్యూస్ పాత్రను పోషిస్తుంది; అందువల్ల, దాని పొడవును కనుగొనడానికి, మేము పైథాగరియన్ సిద్ధాంతాన్ని వర్తింపజేస్తాము. ఫలితంగా, ఈ సూత్రం ఎన్ని భాగాలతోనైనా వెక్టర్లకు సులభంగా వర్తిస్తుంది.
   • || యు || = యు₁ + యు₂. వెక్టర్ రెండు భాగాలకు మించి ఉంటే, + u ని జోడించడం కొనసాగించండి₃ + యు₄ +...
   • అందువల్ల, రెండు డైమెన్షనల్ వెక్టర్ కోసం, మేము చేయవలసి ఉంటుంది || యు || = √ (యు₁ + యు₂).
   • మా ఉదాహరణలో, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   రెండు వెక్టర్ల మధ్య స్కేలార్ ఉత్పత్తిని లెక్కించండి. వెక్టర్లను గుణించే పద్ధతిని మీరు ఇప్పటికే తెలుసుకోవాలి స్కేలార్ ఉత్పత్తి. రెండు వెక్టర్స్ యొక్క స్కేలార్ ఉత్పత్తిని వాటి భాగాల పరంగా లెక్కించడానికి, మేము భాగాలను ఒకదానితో ఒకటి ఒకే దిశలో గుణించి, ఆ ఉత్పత్తుల ఫలితాలను జోడిస్తాము.
   • మీరు కంప్యూటర్ గ్రాఫిక్స్ ప్రోగ్రామ్‌లతో పని చేస్తే, ముందుగా కొనసాగడానికి ముందు "చిట్కాలు" విభాగాన్ని సందర్శించండి.
   • గణిత పరంగా, • = యు₁v₁ + యు₂v₂, ఇక్కడ u = (u₁, యు₂). మీ వెక్టర్‌లో రెండు కంటే ఎక్కువ భాగాలు ఉంటే, + u ని జోడించడం కొనసాగించండి₃v₃ + యు₄v₄...
   • మా ఉదాహరణలో, • = u₁v₁ + యు₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. ఇది వెక్టర్స్ మరియు మధ్య స్కేలార్ ఉత్పత్తి యొక్క విలువ.

5. 

   ఈ ఫలితాలను కొసైన్ సూత్రంలో ప్రత్యామ్నాయం చేయండి. గుర్తుంచుకోండి, cosθ = (•) / (|||| || ||). మేము ఇప్పటికే స్కేలార్ ఉత్పత్తిని మరియు రెండు వెక్టర్స్ యొక్క మాడ్యూల్‌ను లెక్కించాము. ఇప్పుడు, ఈ విలువలను సూత్రంలో భర్తీ చేద్దాం మరియు కోణం యొక్క కొసైన్ను లెక్కించండి.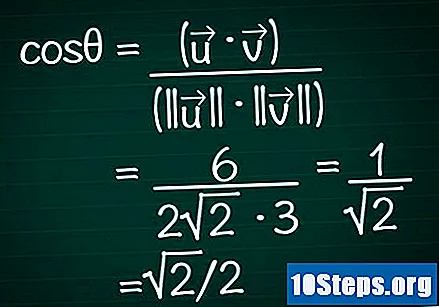
   • మా ఉదాహరణలో, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   మీ కొసైన్ ఆధారంగా కోణాన్ని కనుగొనండి.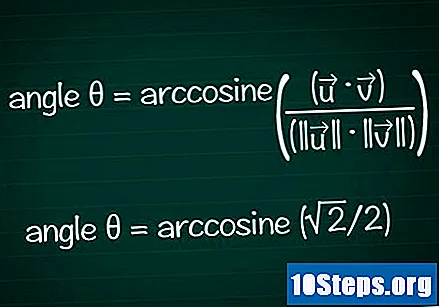
   మీ కొసైన్ విలువ నుండి కోణాన్ని నిర్ణయించడానికి మీ కాలిక్యులేటర్ యొక్క ఆర్క్ లేదా కాస్ ఫంక్షన్‌ను ఉపయోగించండి. కొన్ని సందర్భాల్లో, మీరు యూనిట్ సర్కిల్ ఆధారంగా కోణ విలువను కనుగొనగలుగుతారు.
   • మా ఉదాహరణలో, cosθ = √2 / 2. కోణాన్ని కనుగొనడానికి మీ కాలిక్యులేటర్‌లో "ఆర్కోస్ (√2 / 2)" అని టైప్ చేయండి. Cosθ = √2 / 2 ఉన్న యూనిట్ సర్కిల్ యొక్క కోణం for కోసం చూడటం మరొక ఎంపిక: ఇది దీనికి నిజం అవుతుంది θ = /₄ లేదా 45 °.
   • మొత్తం సమాచారాన్ని కలిపి చూస్తే, మనకు final = ఆర్కోసిన్ ((•) / (|||| || ||) తుది సూత్రం ఉంటుంది.

2 యొక్క 2 వ భాగం: కోణాన్ని లెక్కించడానికి సూత్రాన్ని నిర్వచించడం

1. 

   సూత్రం యొక్క ఉద్దేశ్యాన్ని అర్థం చేసుకోండి. రెండు వెక్టర్ల మధ్య కోణాన్ని లెక్కించడానికి మేము ఉపయోగించిన సూత్రం ముందుగా ఉన్న నియమాల నుండి తీసుకోబడలేదు; బదులుగా, ఇది రెండు వెక్టర్స్ మరియు వాటి మధ్య కోణం మధ్య స్కేలార్ ఉత్పత్తి యొక్క నిర్వచనంగా సృష్టించబడింది. అయితే, ఈ నిర్ణయం ఏకపక్షంగా లేదు. ప్రాథమిక జ్యామితిని నిశితంగా పరిశీలిస్తే, ఈ ఫార్ములా ఎందుకు ఉపయోగకరమైన మరియు సహజమైన నిర్వచనాలకు దారితీస్తుందో మనం చూడవచ్చు.
   • కింది ఉదాహరణలు రెండు డైమెన్షనల్ వెక్టర్లను ఉపయోగించుకుంటాయి ఎందుకంటే అవి పని చేయడానికి చాలా సహజమైన రకం. మూడు లేదా అంతకంటే ఎక్కువ కొలతలు కలిగిన వెక్టర్స్ వాటి లక్షణాలను సాధారణ సూత్రం నుండి నిర్వచించాయి (చాలా సారూప్య మార్గంలో కూడా).

2. 

   కొసైన్ చట్టాన్ని సమీక్షించండి. ఏదైనా త్రిభుజంలో, భుజాలు ఏర్పడిన కోణాన్ని పరిగణించండి ది మరియు B మరియు వైపు ç ఆ కోణానికి ఎదురుగా. కొసైన్ చట్టం ప్రకారం, c = a + b -2abదట్టి(Θ). ఈ ఫార్ములా యొక్క ప్రదర్శన ప్రాథమిక జ్యామితి పరిజ్ఞానం నుండి సులభంగా పొందవచ్చు.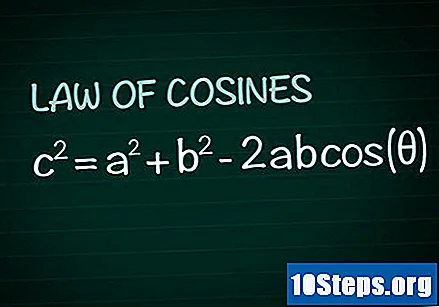

3. 

   త్రిభుజం ఏర్పడటానికి రెండు వెక్టర్లను కనెక్ట్ చేయండి. ఒక జత వెక్టర్లను గీయండి మరియు వాటి మధ్య an కోణంతో. అప్పుడు, త్రిభుజం ఏర్పడటానికి వాటి మధ్య మూడవ వెక్టర్ గీయండి. మరో మాటలో చెప్పాలంటే, వెక్టర్‌ను + = లేదా సరళంగా = - గీయండి.

4. 

   ఈ త్రిభుజానికి కొసైన్ చట్టాన్ని వర్తించండి. మా వైపులా పొడవును భర్తీ చేయండి వెక్టర్ త్రిభుజం (అంటే, వెక్టర్ మాడ్యూల్) కొసైన్ చట్టం యొక్క సూత్రంలో:
   • || (అ - బి) || = || అ || + || బి || - 2 || అ || || బి ||దట్టి(θ)

5. 

   స్కేలార్ ఉత్పత్తులను ఉపయోగించి సూత్రాన్ని తిరిగి వ్రాయండి. డాట్ ఉత్పత్తి ఒక వెక్టార్ యొక్క విస్తరణ మరొకదానిపై అంచనా వేయబడిందని గుర్తుంచుకోండి. వెక్టర్ యొక్క స్కేలార్ ఉత్పత్తికి ప్రొజెక్షన్ అవసరం లేదు ఎందుకంటే దిశలో మార్పు లేదు. దీని అర్థం • = || అ ||. ఈ సమాచారం ఆధారంగా, కొసైన్ చట్టం యొక్క సమీకరణాన్ని తిరిగి వ్రాద్దాం:
   • (-) • (-) = • + • - 2 || అ || || బి ||దట్టి(θ)

6. 

   సూత్రాన్ని సరళీకృతం చేయండి. సమీకరణం యొక్క ఎడమ వైపున ఉన్న ఉత్పత్తులను విస్తరించండి మరియు కోణాలను లెక్కించడానికి మాకు తెలిసిన సూత్రాన్ని మీరు చేరే వరకు దాన్ని సరళీకృతం చేయండి.
   • • - • - • + • = • + • - 2 || అ || || బి ||దట్టి(θ)
   • - • - • = -2 || అ || || బి ||దట్టి(θ)
   • -2 (•) = -2 || అ || || బి ||దట్టి(θ)
   • • = || అ || || బి ||దట్టి(θ)

చిట్కాలు

• శీఘ్ర రిజల్యూషన్ కోసం, కింది సూత్రాన్ని ఏదైనా రెండు డైమెన్షనల్ వెక్టర్ జతకి వర్తించండి: cosθ = (u₁ • v₁ + యు₂ • v₂) / ((యు₁ • u₂) • √ (వి₁ • v₂)).
• మీరు కంప్యూటర్ గ్రాఫిక్స్ ప్రోగ్రామ్‌లతో పని చేస్తే, మీరు వెక్టర్స్ యొక్క దిశను మాత్రమే తెలుసుకోవాలి, వాటి పొడవు కాదు. సమీకరణాలను సరళీకృతం చేయడానికి మరియు మీ ప్రోగ్రామ్‌ను వేగవంతం చేయడానికి క్రింది దశలను అనుసరించండి:
  • ప్రతి వెక్టర్‌ను సాధారణీకరించండి, అనగా, అసలు వెక్టార్‌కు సమానమైన దిశను కలిగి ఉన్న యూనిట్ వెక్టర్‌ను కనుగొనండి. ఇది చేయుటకు, వెక్టర్ యొక్క ప్రతి భాగాన్ని వెక్టర్ మాడ్యూల్ ద్వారా విభజించండి.
  • అసలు వెక్టర్స్ కాకుండా సాధారణీకరించిన వెక్టర్స్ యొక్క స్కేలార్ ఉత్పత్తిని లెక్కించండి.
  • సాధారణీకరించిన వెక్టర్స్ యొక్క మాడ్యులస్ (అంటే, పొడవు) ఏకీకృతం కనుక, మేము వాటిని ఫార్ములా నుండి వదిలివేయవచ్చు. కోణాలను లెక్కించడానికి మీ చివరి సమీకరణం ఆర్క్స్ (•) అవుతుంది.
• కొసైన్ చట్టం యొక్క సూత్రం ఆధారంగా, ప్రశ్నలోని కోణం తీవ్రమైనదా లేదా అస్పష్టంగా ఉందా అని మనం త్వరగా తెలుసుకోవచ్చు. Cosθ = (•) / (|||| ||||) తో ప్రారంభించండి:
  • సమీకరణం యొక్క ఎడమ మరియు కుడి వైపులా ఒకే గుర్తు ఉండాలి (సానుకూల లేదా ప్రతికూల).
  • పొడవు ఎల్లప్పుడూ సానుకూలంగా ఉన్నందున, cosθ ఎల్లప్పుడూ స్కేలార్ ఉత్పత్తికి సమానమైన చిహ్నాన్ని కలిగి ఉంటుంది.
  • అందువల్ల, స్కేలార్ ఉత్పత్తి సానుకూలంగా ఉంటే, cosθ సానుకూలంగా ఉంటుంది. దీని అర్థం కోణం యూనిట్ సర్కిల్ యొక్క మొదటి క్వాడ్రంట్లో ఉంటుంది, అంటే θ <π / 2 లేదా 90 °. కాబట్టి, కోణం తీవ్రంగా ఉంటుంది.
  • స్కేలార్ ఉత్పత్తి ప్రతికూలంగా ఉంటే, cosθ ప్రతికూలంగా ఉంటుంది. దీని అర్థం కోణం యూనిట్ సర్కిల్ యొక్క రెండవ క్వాడ్రంట్లో ఉంటుంది, అనగా π / 2 <θ 90 π లేదా 90 ° <θ ≤ 180 °. అందువల్ల, కోణం అస్పష్టంగా ఉంటుంది.